Количество шпал на на 1 км и порядок их расположения по длине рельсового звена (эпюра укладки) нормируется исходя из условий выравнивания давлений в балластном слое по его глубине, а также обеспечения необходимой сопротивляемости рельсошпальной решетки продольному и поперечному сдвигу. В результате экспериментальных и теоретических исследований установлено, что при расстоянии между осями смежных шпал 60 см (при эпюре 1600 шт/км) полное выравнивание напряжений происходит на глубине около 75 см (больше нормативной) под подошвой шпал.

Максимально е погонное сопротивление ресошпальной решетки сдвигу в щебеночном балласте вдоль пути имеет место при ширине шпального пролета 50-51 см. Поэтому увеличение числа шпал более 2000 шт/км не влияет на устойчивость пути против продольных смещений.

Указанные критерии, наряду с экономическими соображениями, послужили основанием для назначения двух основных стандартных эпюр укладки шпал, соответствующих 1840 шт/км (46 шпал в 25-метровом звене) в прямых и кривых радиусом более 1200 м и 2000 шт/км (50 шпал на звене) в кривых радиусом 1200 м и менее (на скоростных линиях при v>141 км/ч в кривых радиусом 2000 и менее).

На путях 5-го класса допускается эпюра шпал в прямых 1440 шт/км, а вкривых радиусом менее 650 м - 1600 шт./км (40 шпал на звене).

Для улучшения условий работы пути под поездной нагрузкой в зоне рельсовых стыков стыковые шпалы сближаются друг с другом. При всех эпюрах расстояния между осями стыковых шпал стандартные: 42 см при рельсах Р65, Р75 и 44 см при рельсах Р50.

Расстояния между осями остальных шпал на протяжении рельсового звена одинаковы и равны 54,6 см (эпюра 1840 шт./км) и 50,2 (2000 шт./км)

Назначенные расстояния между осями шпал в соответствии с эпюрой должны удовлетворять следующим условиям:

прочность рельса при расчете на изгиб;

статический расчет давления на балласт и основную площадку земляного полотна.

Статический расчёт рельса на изгиб как неразрезной балки на сплошном упругом основании.

Число опор, вводимое в расчет рельса как многопролетной неразрезной балки на упругих точечных опорах, ограничивается условием, чтобы влияние наиболее удаленных грузов и реакций крайних опор на величину изгибающего момента в рассматриваемом сечении было близко к нулю.

Из ряда опытов установлено, что это влияние оказывается практически ничтожным при выделении участка рельса с 10-11 пролетами при сосредоточенной нагрузке по середине участка балки.

(8.51)

в случае действия одичночной нарузки P и

(8.52)

(8.53)

в случае действия системы грузов Рi.

Здесь µ - ординаты инфлюэнтных линий изгибающего момента по середине шпального пролета в середине рельсового звена и η – ординаты инфлюэнтных линий давления на средние опоры рельса.

Значения η и µ приводятся в таблицах в зависимости от относительных расстояний x/l и коэффициентов l/γ,

где х – расстояние от груза до рассматриваемого сечения;

l – расстояние между осями шпал;

γ – так называемый коэффициент относительной жесткости рельса и опоры.

(8.54)

Здесь D – величина, характеризующая упругие свойства шпалы и основания.

(8.55)

где С – коэффициент постели шпал;

а – длина шпалы;

b – ширина нижней постели шпалы;

α – коэффициент изгиба шпалы, равный

(8.56)

Статический расчет давления на балласт и основную площадку земляного полотна.

Наибольшие давления на балластный слой возникает непосредственно под подошвой шпалы и распространяется на некоторую глубину в сечениях под рельсами.

Средняя величина давления

(8.57)

где α – коэффициент изгиба шпалы;

а и b – длина и ширина шпалы;

Q – давление на шпалу.

Напряжение σh в балласте на некоторой глубине h>15 см под подошвой шпалы, а также напряжение. возникающее нна основней площадке земляного полотна, определяют по формуле

(8.58)

где σh’ - напряжение, обусловленное давлением на балласт от основной расчетной шпалы;

σh’’ - напряжение, обусловленное давлением на балласт от одной шпалы, лежащей рядом с расчетной;

σh’’’ - напряжение, обусловленное давлением на балласт от другой соседней шпалы;

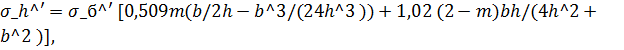(8.59)

где - средняя величина напряжения в балластном слое под расчетной шпалой на уровне подошвы шпалы;

m – коэффициент концентрации, равный

(8.60)

(8.61)

(8.62)

где:

(8.63)

σб’ и σб’’ – среднее напряжение в балласте под соседними с расчетной шпалами на уровне подошвы;

l – расстояние между осями шпал.